Figuri geometrice de rotație

Cilindru

Chiar într-un proiect recent la geografi am avut nevoie să utilizez cilindru pentru calcularea energii primite dintr-o turbină eoliană.

Știm că turbina transformă energia vîntului în cea electrică, deci calculînd energia vîntului putem calcula cantitatea de electricitate generată de turbină. Noi știm că energia generată nu poate depăși energia vîntului, aceasta ar însemna că energia apare din nimic, ceea ce violează legile conservării energiei.(Legile date nu sunt ca niște promisiune spuse de mine. Sunt legi cărora li se supune tot ce există.)

Energia(cinetică) a vîntului poate fi calculată cu relația E_c=\frac{m\cdot v^2}{2}, unde m este masa aerului care antrenează elicile turbinei, iar v este viteza masei de aer. Masa de aer poate fi calculată dacă îmi vom imagina aerul ca un cilindru, baza fiind cercul descris de elicea efectînd o revoluție, iar înalțimea fiind distanța parcursă de vînt într-un timp t dat, exemplificat în imaginea de mai jos.

Suprafața lovită de aer v-a fi:

Volumul de aer care v-a lovi turbina, se v-a calcula dupa relația de calcularea volumului unui cilindru:

Unde distanța este d = v \cdot t:

Masa va fi produsul dintre volumul și densitatea aerului (\rho=1.225 \frac{kg}{m^3})

Din acestea deducem relația:

E_c=\frac{\pi \cdot r^2 \cdot t \cdot \rho \cdot v^3}{2}

Unde pentru simplitate t = 1s

E_c=\frac{\pi \cdot r^2 \cdot \rho \cdot v^3}{2}

Drept într-o lume perfectă, unde nu-s de loc pierderi de energie și unde eu finisez la timp proiectele, o turbină eoliană cu elicea de 1m și la viteza de 2m/s v-a produce ~15,4J timp de o secundă, sau ~15.4W.

Sfera

Din cauza că pămîntul este rotund, obiectele de aceiași lungime, pe același meridian, perpendiculare pe pămînt, vor avea lungimi de umbre diferite.

Cu ajutorul acestui fenomen se poate de calculat circumferința pămîntului(pe meridianul dat). Defapt aceasta și a făcut-o matimaticianul grec Eratostene¹.

La momentul solstițiului de vară (21 iunie), la ora 12:00, cînd razele solare cădeau perpendicular pe localitatea Assuan. La aceeași dată și oră, în orașul Alexandria, situat aproximativ pe același meridian ca și Assuan (diferență de 2 \degree), umbra lăsată de un turn reprezenta \frac{1}{50} din circumferința unui cerc. Aceasta corespunde unui unghi de aproximativ 7 \degree 12’. Distanța dintre acestea localități era de aproximativ 800km (5000 stadii). Astfel, un cerc mare al sferei cu care era aproximat Pământul era de cca 50 \cdot 5.000 = 250.000stadii \approx 39.690km.²

Con

Vom calcula suprafața de hîrtie necesară pentru a creea un con.

Un motan poate avea circumferința capului de aproximativ 23-28cm. Desigur în dependență de specie. Vom creea un con pentru un motan cu circumferința capului de 25cm.

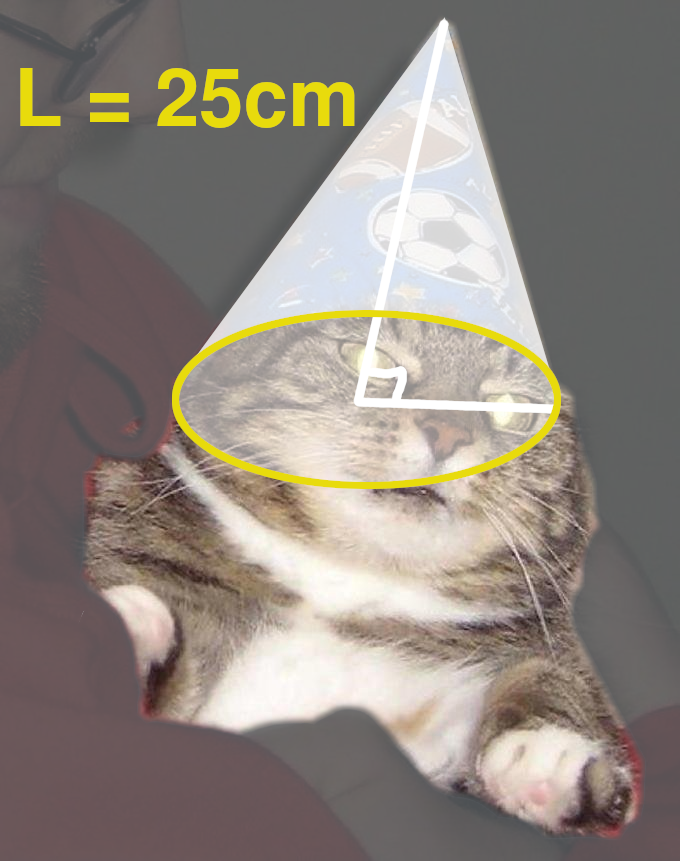
Din relația pentru circumferința cercului L_c = 2\cdot \pi \cdot r , putem afla raza

r = \frac{L_c}{2\cdot \pi} = \frac{25cm}{2\cdot \pi} = 3.66cm

Înălțimea o putem lua după dorință. În cazul meu doresc conul să fie de 10cm. Pentru a afla aria laterală a conului avem nevoie și de generatoare lui. Acum că știm înălțimea și raza o putem afla prin teoreama lui Pitagora.

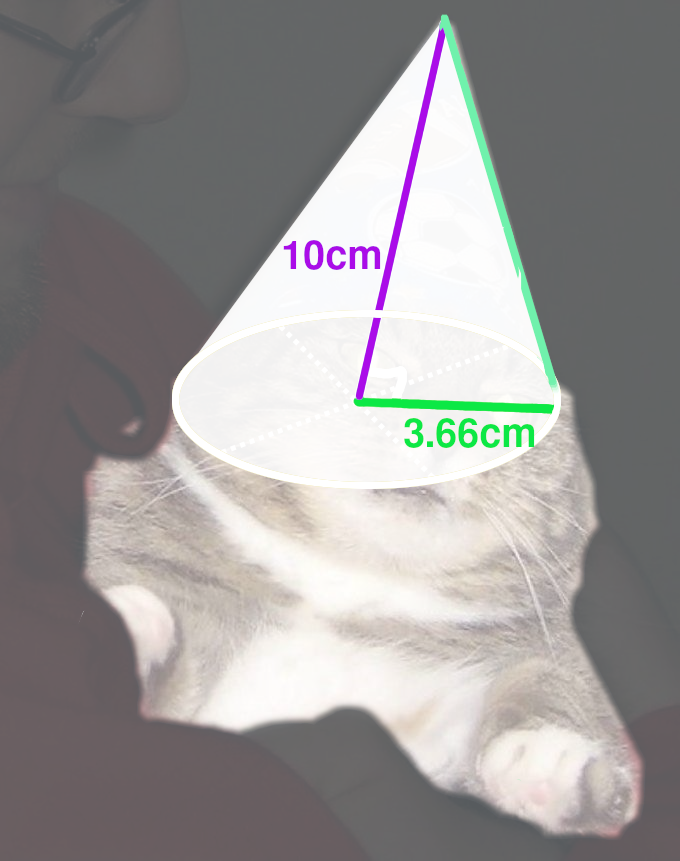
De acum putem simplu afla aria laterală a conului.

Trebuie să luăm în considerare și restul de hîrtie care-l vom utiliza pentru lipirea conului